Yifan Chen, Xiaoxia Wang: Some Lucas-like congruences for $q$-trinomial coefficients, 417-427

Abstract:

In this paper, we present several new $q$-congruences on the $q$-trinomial coefficients introduced by Andrews and Baxter. As a conclusion, we obtain the following congruence:

$$\Bigg(\!\!\binom{ap+b}{cp+d}\!\!\Bigg)\equiv\Bigg(\!\!\binom{a}{c... ...)+\Bigg(\!\!\binom{a}{c+1}\!\!\Bigg)\Bigg(\!\!\binom{b}{d-p}\!\!\Bigg)\pmod{p},$$

where $a,b,c,d$ are integers subject to $a \geq 0, 0 \leq b,d \leq p-1$, and $p$ is an odd prime.

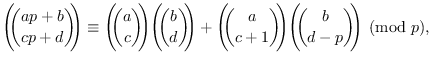Besides, we find that the method can also be used to reprove Pan's Lucas-type congruence for the $q$-Delannoy numbers.

Key Words: $q$-trinomial coefficients, $q$-congruences, cyclotomic polynomials.

2020 Mathematics Subject Classification: Primary 11B65; Secondary 33C20, 11A07.

Download the paper in pdf format here.